The mathematician John Baez has been dazzling science lovers on the web for over 15 years with his weekly Finds in Mathematical Physics. (He was a blogger long before there were blogs). Baez recently gave a lovely series of talks on his favorite numbers (they are 5, 8 and 24) in which he mentions Euler’s observation that if you sum up all the positive integers (1 + 2 + 3 + 4 + …) you get -1/12. (I promise, this is not a joke.)
Baez’s “proof” uses a little calculus, but I’ve reworked it into a form you can share with your middle schoolers—and better yet, have them share with their teachers.
Step One. Let’s compute something easier, like 1 – 1 + 1 – 1 + 1 … . Start by making up a name for this sum; let’s call it N. If we add N to itself—and if we line up the columns in the right way — we get 1:
Image may be NSFW.
Clik here to view.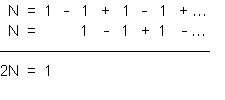
So that tells us that N = 1/2.
Step Two. Now let’s try squaring N. We want to compute N times N, which we can write as N(1-1+1-1+1-1+…) = N-N+N-N+N… and here’s that computation:
Image may be NSFW.
Clik here to view.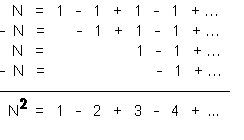
But we already know that N=1/2, so this tells us that 1-2+3-4+… = (1/2)2 = 1/4.
Step 3. Now let’s turn to the sum we’re really interested in; 1 + 2 + 3 + 4 + … . Call this M. Then 4M = 4 + 8 + 12 + 16 + … . And if we line things up right and then subtract, we get
Image may be NSFW.
Clik here to view.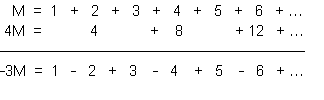
In other words (using Step Two), -3M = 1/4, whence M = -1/12. Voila.
Now of course, as your child’s middle school teacher will insist, there’s nothing legitimate about any of this; if you line up your columns right, you can prove anything at all. What’s remarkable, though, is that Euler had phenomenal instincts about how to line up his columns. There is a very deep sense in which -1/12 is exactly the right answer to this problem. Here is a hint of why (warning: this link is WAY too technical for your middle schooler, and for almost everyone else).
Nor is this a purely mathematical game; the physical world seems to care about such calculations. When you try to calculate the energy in, say, a tiny vibrating string, you tend to come up with answers like 1+2+3+4+… You might say “that’s infinite”, but the notion of infinite energy sounds like nonsense to a physicist. On the other hand, an energy of -1/12—well, you might think that sounds like equal nonsense. Strangely, though, you’d be wrong. By taking such results seriously, physicists have been led to deep and meaningful theories. (If you have a taste for advanced mathematics, you can learn more about this in Baez’s talk or the associated slides.)
And so we have one more example of the (apparently) unreasonable effectiveness of pure mathematics —indeed, mathematics at its purest—as a description of the physical world—a recurring theme in The Big Questions.
